La ley de ohm.
El físico Georg Simón Ohm dictaminó: la corriente que circula por un circuito eléctrico cerrado, es directamente proporcional a la tensión que tiene aplicada, e inversamente proporcional a la resistencia que ofrece a su paso la carga que tiene conectada.Que expresado de forma ecuacional:
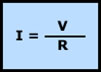
Donde:
I= es la intensidad.
V= es la tensión.
R= es la resistencia.
Es evidente que teniendo dos de las tres magnitudes podemos averiguar la tercera con facilidad. En honor al físico, la unidad de la resistencia es el ohm.
El efecto Joule.
Cuando la electricidad circula o pasa por un conductor o una resistencia, se produce un calor. A este calor producido se le denomina El efecto de Joule.El físico James Prescott Joule en un experimento realizado con un calorímetro dictaminó que 1 Julio es igual a 0,24 calorías. Es decir, realizó un experimento sobre la energía (julio) transformada plenamente en calor (caloría).
Así tenemos que:

Donde:
Q= Calor.
E= Energía.
Esta fórmula, puesta de esta manera, poca utilidad le puede sacar un eléctrico. Pero si la combinamos con la potencia y el tiempo: E=P*t y P=R*I2 tendremos una ecuación más útil para un eléctrico:

Donde:
Q= Calor.
R= Resistencia.
I= Intensidad.
t= Tiempo.
El calor específico.
Al calor específico se la llama a la cantidad de calor necesaria para aumentar 1°C la temperatura de 1 gramo de cualquier sustancia.Existen multitud de tablas físicas donde salen los valores calóricos de multitud de sustancias. Aún así, os dejo la fórmula por si os falta el valor del calor específico:

Donde:
Q= Cantidad de calor.
m= Masa.
c= Calor específico.
Δt= Variación del tiempo.
Las leyes de Kirchhoff.
Cuando tenemos circuitos eléctricos con más de una pila o generador se tienen que aplicar las leyes de Kirchhoff para poder resolver el circuito. Existen dos leyes de Kirchhoff:1. Ley de Kirchhoff.
Dice: "la suma de las intensidades que van hacia un nudo es igual a la suma de las intensidades que se alejan del mismo nudo."
¿Os acordáis de aquella máxima de física de que la suma de todas las fuerzas es igual a cero? Pues con la primera ley de Kirchhoff sucede exactamente lo mismo.
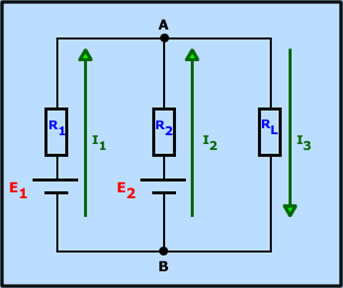
En este dibujo podemos observar que existen dos nudos: A y B.
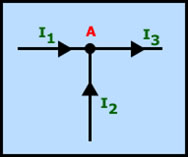
En este gráfico se puede observar con más claridad. Tanto I1 como I2 se acercan al nudo que llamamos A, sin embargo, I3 se aleja del nudo. Así, que la primera ley de Kirchhoff será:
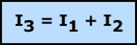
Nota: Con el nudo B sucedería a la inversa, es decir, la I3 entra en el nudo B, mientras, que I2 y I1 salen del nudo B.
2. Ley de Kirchhoff.
Esta segunda ley de Kirchhoff hace referencia a las tensiones.
Aquí tenemos que explicar primero el concepto de malla. Y para ello nos vamos a servir del mismo dibujo de arriba:

En este dibujo podemos observar dos mallas:
1ª Malla. Es la que comprende los elementos: E1, R1, R2 y E2.
2ª Malla. Es la que comprende los elementos: E2, R2 y RL.
Como podéis ver las mallas son como subcircuitos cerrados dentro del mismo circuito. Esto es importante saberlo y, sobretodo, saber identificar cada malla. Para ello, basta en señalar los nudos del circuito y seguir las corrientes que producen los generadores o pilas.
Pues bien, ahora que ya sabemos lo que es una malla podemos enunciar la segunda ley de Kirchhoff: "En una malla la suma de todas las diferencias de potencial es igual a cero".

En este dibujo observamos de que manera hemos resuelto las polaridades o los signos positivos y negativos. Este dato es importante hacerlo porque de otra manera no resolveriamos satisfactoriamente las ecuaciones. Para ello, hemos seguido la f.e.m. del propio generador o pila. Obtenemos la siguiente ecuación:
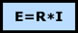
No hay comentarios:
Publicar un comentario