En
cinemática, el
movimiento circular (llamado también
movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la
trayectoria es una
circunferencia. Si, además, la velocidad de giro es constante, se produce el
movimiento circular uniforme, que es un caso particular de movimiento circular, con radio fijo y velocidad angular constante.
En los movimientos circulares hay que tener en cuenta algunos conceptos específicos para este tipo de movimiento:
- Eje de giro: es la línea alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo, pero para cada instante de tiempo, es el eje de la rotación.
- Arco: partiendo de un eje de giro, es el ángulo o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián.
- Velocidad angular: es la variación de desplazamiento angular por unidad de tiempo.
- Aceleración angular: es la variación de la velocidad angular por unidad de tiempo.
En
dinámica del movimiento giratorio se tienen en cuenta además:
- Momento de inercia: es una cualidad de los cuerpos que resulta de multiplicar una porción de masa por la distancia que la separa al eje de giro.
- Momento de fuerza: o par motor es la fuerza aplicada por la distancia al eje de giro.
[editar] Paralelismo movimiento lineal–angular
A pesar de las diferencias, hay ciertas similitudes entre el movimiento lineal y circular, que son dignos de destacar, y que deja a las luces las similitudes en la estructura y un paralelismo en las magnitudes. Dado un eje de giro y la posición de una partícula en movimiento giratorio, para un instante
t, dado, se tiene:
Arco angular o
posición angular es el
arco de la
circunferencia, medido en
radianes, que realiza un giro, se lo representa con la letra
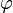
.
Si se llama
e al espacio recorrido, a lo largo de la circunferencia de radio
R, se tiene que:
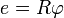
[editar] Velocidad angular y tangencial
Velocidad angular es la variación del arco respecto al tiempo, se lo representa con la letra
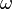
, se define como:
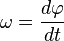
Velocidad tangencial de la partícula es la velocidad del objeto en un instante de tiempo. Puede calcularse a partir de la velocidad angular. Si
vt es la velocidad tangencial, a lo largo de la circunferencia de radio
R, se tiene que:
 .
.
[editar] Aceleración angular
La
aceleración angular es la variación de la
velocidad angular por unidad de tiempo y se la representa con la letra:

y se la calcula:
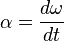
Si
at es la
aceleración tangencial, a lo largo de la circunferencia de radio
R, se tiene que:

[editar] Período y frecuencia
El
período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:

La
frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en
hercios o s
-1

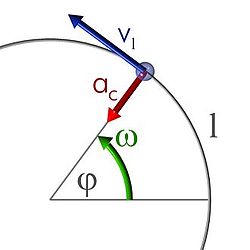
[editar] Aceleración y fuerza centrípeta
La
aceleración centrípeta o aceleración normal afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:
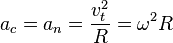
La
fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la
masa del móvil, y basándose en la
segunda ley de Newton (

) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
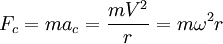
[editar] Véase también
 .
.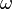 , se define como:
, se define como: y se la calcula:
y se la calcula: ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación: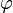 .
.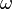 , se define como:
, se define como:.
 y se la calcula:
y se la calcula: ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente relación:
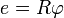
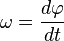
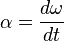



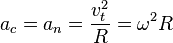
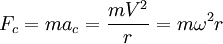
No hay comentarios:
Publicar un comentario